-
Diketahui y =
. Jika y
1 +
dan 0
x
2
, maka nilai x yang memenuhi adalah ….
(A) 0 < x <
(B) 0 < x
(C) 0
x
(D) 0 < x
(E) 0 < x <
PEMBAHASAN :
y
1 +
y – 1 +
0
+
0
0
pembilang :
y =
y = sin x
y2 – y + 2
0
(y + 1)(y – 2)
0
y = -1 atau y = 2
sin x = 2 (tidak ada x yang memenuhi)
sin x = -1
x =
penyebut :
y < 0
sin x < 0
x = 0,
,
dengan menggunakan garis bilangan, diperoleh
0 < x <
atau
x <
JAWABAN :
-
= ….
(A) 1/4
(B) 1/2
(C) 1
(D) 2
(E) 4
PEMBAHASAN :
=
=
=
1.
= 1
JAWABAN : C
-
Dari sehelai karton akan dibuat sebuah kotak tanpa tutup dengan alas persegi. Jika jumlah luas bidang alas dan semua bidang sisi kotak adalah 192 cm2, maka volume kotak terbesar yang mungkin adalah ….
(A) 256 cm3
(B) 320 cm3
(C) 364 cm3
(D) 381 cm3
(E) 428 cm3
PEMBAHASAN :
Luas = luas alas + 4 luas sisi
192 = s2 + 4st
(192 – s2)/4s = t
V = s2[(192 – s2)/4s]
= (192s2 – s4)/4s
= 48s – s3/4
V’ = 48 – 3s2/4
0 = 48 – 3s2/4
48s = 3s2/4
s = 8cm
192 = s2 + 4st
t = (192 – s2)/4s
= (192 – 82)/4.8
= 4cm
Volume = s2t
= (8 cm)2 4 cm
= 256 cm3
JAWABAN : A
-
Jika diketahui xyz = 26 dan (2log x)(2log yz) + (2log y)(2log z) = 10 dengan x, y, z
0, maka
= ….
(A) 2
(B) 3
(C) 4
(D) 5
(E) 6
PEMBAHASAN :
xyz = 26
2log (xyz) = 2log 26
2log x + 2log y + 2log z = 6
(2log x)(2log yz) + (2log y)(2log z) = 10
(2log x)(2log y + 2log z) + (2log y)(2log z) = 10
2log x 2log y + 2log x 2log z + 2log y 2log z = 10
misal : a = 2log x, b = 2log y, c = 2log z
maka diperoleh
a + b + c = 6
ab + ac + bc = 10
=
=
=
=
=
= 4
JAWABAN : C
-
Jika diketahui
a + b + c = 18
a2 + b2 + c2 = 756
a2 = bc
maka a = ….
(A) -18
(B) -12
(C) 1
(D) 12
(E) 18
PEMBAHASAN :
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2ac + 2bc
(18)2 = 756 + 2ab + 2ac + 2a2
(18)2 = 756 + 2a(b + c) + 2a2
(18)2 = 756 + 2a(b + c + a)
(18)2 = 756 + 2a(18)
324 = 756 + 36a
-432 = 36a
-12 = a
JAWABAN : B
-
Jika kedua akar persamaan px2 + 8x + 3p = 0 bernilai negatif, maka jumlah kuadrat kedua akar-akar tersebut akan bernilai ….
(A) maksimum 30
(B) minimum 30
(C) minimum 6
(D) maksimum 6
(E) minimum -15/2
PEMBAHASAN :
px2 + 8x + 3p = 0
x1,2 =
=
=
=
=
=
Karena memiliki dua akar rill (keduanya negatif), maka 16 – 3p2
0
16 – 3p2
0
p
p
ambil p =
x1,2 =
=
=
x1 = x2 =
(tidak memenuhi karena nilai x1,2 positif)
(x1)2 + (x2)2 = 2
= 2
= 2 (3)
= 6
ambil p =
x1,2 =
=
=
(x1)2 + (x2)2 = 2
= 2
= 2 (3)
= 6
ambil p = 2 (sebagai pembanding utuk menentukan maks atau min)
x1,2 =
=
=
(x1)2 + (x2)2 = (-1)2 + (-3)2
= 1 + 9
= 10
dapat disimpulkan bahwa 6 adalah nilai minimum.
JAWABAN : C
-
Apabila k = x + y, maka k2 – k = 1 dan apabila k = x – y, maka k2 + k = 1, maka x + y = …
(1)
(2)
(3)
(4)
PEMBAHASAN :
k2 – k = 1
(x + y)2 – (x + y) = 1
x2 + 2xy + y2 – x – y = 1 … (i)
k2 + k = 1
(x – y)2 + (x – y) = 1
x2 – 2xy + y2 + x – y = 1 … (ii)
(i) – (ii) = 4xy – 2x = 0
2x(2y – 1) = 0
2x = 0 atau 2y – 1 = 0
x = 0 y = 1/2
x + y = 0 + 1/2
= 1/2
k2 – k = 1
k2 – k – 1 = 0
k1,2 =
=
=
k1 =
atau
k2 =
(ingat : k = x + y)
JAWABAN : A
-
Misalkan f : R
R dan g : R
R, f(x) = x + 2 dan (g o f)(x) = 2x2 + 4x – 6. Misalkan juga x1 dan x2 adalah akar-akar dari g(x) = 0, maka x1 + 2x2 = ….
(1) 0
(2) 1
(3) 3
(4) 5
PEMBAHASAN :
f(x) = x + 2
f-1(x) = y – 2 = x – 2
g (x) = (g o I)(x)
= (g o f o f-1)(x)
= ((g o f) o f-1)(x)
= (g o f)(f-1(x))
= (g o f)(x – 2)
= 2(x – 2)2 + 4(x – 2) – 6
= 2(x2 – 4x + 4) + 4x – 8 – 6
= 2x2 – 8x + 8 + 4x – 8 – 6
= 2x2 – 4x – 6
g(x) = 0
2x2 – 4x – 6 = 0
2(x2 – 2x – 3) = 0
2(x – 3)(x + 1) = 0
x1 = 3 atau x2 = -1
atau
x2 = 3 atau x1 = -1
x1 + 2x2 = 3 + 2(-1) = 1
x1 + 2x2 = -1 + 2(3) = 5
JAWABAN : C
-
Jika diketahui
,
, y – 1 adalah tiga suku barisan aritmatika, maka nilai suku kedua yang memenuhi adalah ….
(1) -1
(2) -2
(3) 1
(4) 2
PEMBAHASAN :
2u2 = u1 + u3
2(
) = (y – 1) –
(y2 + 3y – 1) – (y – 1) = –
y2 + y +
= –
[kuadratin kedua ruas]
y4 + y2 +
+ 2(
y2)(y) + 2(
y2)(
) + 2(3y)(
)) = y2 + 2y + 1
y4 +
y3 +
y2 –
y –
= 0
dengan menggunakan metode horner, diperoleh
y1 = -2, y2 = y3 = -1 atau y4 = 1
untuk y = -2
u2 =
=
=
= -1
untuk y = -1
u2 =
=
=
= -1
untuk y = 1
u2 =
=
=
= 1
JAWABAN : B
-
Diketahui bahwa x2 + 2xy + 2y2 = 13 dengan x dan y adalah bilangan bulat. Nilai x – y yang mungkin dengan x > 0 dan y > 0 adalah ….
(1) 4
(2) 1
(3) -4
(4) -1
PEMBAHASAN :
x2 + 2xy + 2y2 = 13
(x2 + 2xy + y2) + y2 = 13
(x + y)2 + y2 = 13
kemunhgkinan pertama :
x + y = 2 dan y = 3
maka x = -1
sehingga x – y = -4
kemuningkinan kedua :
x + y = 3 dan y = 2
maka x = 1
sehingga x – y = -1
karena persayatannya adalah x > 0 dan y > 0, maka jawaban yang memenuhi syarat adalah x – y = -1
JAWABAN : D
NOTE : silahkan dikoreksi dan berikan komentar jika ada kesalahan atau masih ada keambiguan dalam penyelesaian soal-soal ini.

mas soal no 10 simak ui 2012 [Kode Soal 221] (1), kenapa k yang d ambil k nya -2 dan -1 …?
karena cuma k yang -2 dan -1 yang memenuhi, coba aja km cek kemungkinan yang ada, selain -2 dan -1, tidak memenuhi syarat.
2 dan 1 kenapa gk boleh
coba perhatikan persamaan terakhir
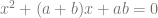
 nya, ketika
nya, ketika 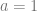 dan
dan  , maka
, maka  , padahal yang kita butuhkan adalah tanda negatif yaitu
, padahal yang kita butuhkan adalah tanda negatif yaitu  , makanya yang memenuhi itu -1 dan -2.
, makanya yang memenuhi itu -1 dan -2.
dan persamaan umum dari persamaan kuadrat
jika kita substitusi 2 dan 1, tidak akan memenuhi di koefesien
Nomor 1 kok y² – y + 2 faktornya (y+1)(y-2)?
Bukannya gak ada faktornya?
klo (y+1)(y-2) = y² – y – 2