Apr 23 2012 Rumus-Rumus Dasar Trigonometri . . . . . . 0.000000 0.000000 Bagikan ini:FacebookTwitterCetakSimpan Sebagai PDFWhatsAppSuka Memuat... Terkait
assalamualaikum ka . aku mau nanya boleh kalo ada soal tuh kaya gni ni Sin2 1◦ + Sin2 3◦ + Sin2 5◦ +…+ Sin2 87◦+ Sin2 89. itu cara.a gimana ka ? trimakasih . Balas
Terima kasih
assalamualaikum ka . aku mau nanya boleh kalo ada soal tuh kaya gni ni
Sin2 1◦ + Sin2 3◦ + Sin2 5◦ +…+ Sin2 87◦+ Sin2 89.
itu cara.a gimana ka ?
trimakasih .
walaikumslam.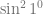 atau
atau  ?
?
itu