Feb 5 2018

Pembahasan TKPA Matematika Dasar SBMPTN 2017 (Kode Soal 226) (2)


  1. Jika f(x) = 1-x^2 dan g(x) = \sqrt{5-x}, maka daerah hasil fungsi komposisi f \circ g adalah …

    A. \{ y~|~ -\infty < y < \infty\}

    B. \{ y~|~ y \leq -1 \text{ atau } y \geq 1\}

    C. \{ y~|~ y \leq 5\}

    D. \{ y~|~ y \leq 1\}

    E. \{ y~|~ -1 \leq y \leq 1\}

    PEMBAHASAN.

    Perhatikan,

    \begin{array}{rl} (f \circ g(x) &= f(g(x))\\ &= f(\sqrt{5-x})\\ &= 1-(\sqrt{5-x})^2\\ &=1-(5-x)\\ &= x-4.\end{array}

    Karena fungsi f \circ g adalah bukan fungsi akar atau rasional (pecahan), maka daerah hasilnya adalah semua bilangan real. Jadi, jawaban yang tepat adalah pilihan A.

    JAWABAN : A

  2. Diketahui kubus ABCD.EFGH dengan P dan Q berturut-turut adalah titik tengah HG dan BC. Jika panjang rusuk kubus tersebut adalah 4 cm, maka jarak P ke Q adalah … cm

    A. 2 \sqrt{3}

    B. 2 \sqrt{6}

    C. 6 \sqrt{2}

    D. 6 \sqrt{3}

    E. 6 \sqrt{6}

    PEMBAHASAN.

    Perhatkan, gambar di atas, diperoleh

    \begin{array}{rl} PP' &= 4\\ CP' &= 2\\ CQ &= 2\\ P'Q &= \sqrt{CP'^2+CQ^2}\\ &= \sqrt{2^2+2^2}\\ &= 2\sqrt{2}\\ PQ &= \sqrt{PP'^2+P'Q^2}\\ &= \sqrt{4^2+(2\sqrt{2})^2}\\ &= \sqrt{16+8}\\ &= \sqrt{24}\\ &= \sqrt{4 \cdot 6} = 2\sqrt{6}. \end{array}

    Jadi, jarak P ke Q adalah 2\sqrt{6} cm.

    JAWABAN : B

  3. Luas daerah penyelesaian sistem pertidaksamaan x+y \leq 3, 3x+2y \geq 6, y \geq 0 adalah … satuan luas

    A. \dfrac{1}{2}

    B. \dfrac{3}{4}

    C. 1

    D. \dfrac{3}{2}

    E. 2

    PEMBAHASAN.

    Dari pertidaksamaan pada soal, diperoleh gambar sebagai berikut,

    titik A adalah perpotongan garis 3x+2y=6 dengan sumbu-x, sehingga diperoleh A(2,0). Kemudian titik B adalah perpotongan garis dengan garis x+y=3, yaitu B(3,0) dan titik C adalah perpotongan garis x+y=3 dengan sumbu-y, yaitu C(0,3). Selanjutnya daerah penyelesaian sistem persamaan merupakan luas egitiga ABC (lihat gambar). Perhatikan,

    \begin{array}{rl} \text{Luas } \triangle OBC &= \dfrac{1}{2} \times OB \times OC\\ &= \dfrac{1}{2} \times 3 \times 3 = \dfrac{9}{2}.\\ \text{Luas } \triangle OAC &= \dfrac{1}{2} \times OA \times OC\\ &= \dfrac{1}{2} \times 2 \times 3 = 3.\\ \text{Luas } \triangle ABC &= \text{Luas } \triangle OBC -\text{Luas } \triangle OAC\\ &= \dfrac{9}{2}-3 = \dfrac{3}{2}. \end{array}

    JAWABAN : D

  4. Titik (1,0) dipetakan dengan translasi \begin{pmatrix} a\\2 \end{pmatrix} dan kemudian dicerminkan terhadap $x=3$ ke titik (6,2). Peta titik (2,1) di bawah transformasi yang sama adalah …

    A. (5,3)

    B. (6,2)

    C. (6,3)

    D. (7,2)

    E. (7,3)

    PEMBAHASAN.

    Translasi terhadap \begin{pmatrix} a\\2 \end{pmatrix} adalah

    \begin{pmatrix} x'\\y' \end{pmatrix} = \begin{pmatrix} 1\\0 \end{pmatrix} + \begin{pmatrix} a\\2 \end{pmatrix} = \begin{pmatrix} 1+a\\2 \end{pmatrix}

    Pencerminan \begin{pmatrix} 1+a\\2 \end{pmatrix} terhadap $x=3$ adalah

    \begin{array}{rl} \begin{pmatrix} x''\\y'' \end{pmatrix} &= \begin{pmatrix} 2h-x\\y \end{pmatrix}\\ \begin{pmatrix} 6\\2 \end{pmatrix} &= \begin{pmatrix} 2(3)-(1+a)\\2 \end{pmatrix}\\ \begin{pmatrix} 6\\2 \end{pmatrix} &= \begin{pmatrix} 5-a\\2 \end{pmatrix} \end{array}

    Dari persamaan terakhir, diperoleh

    6 = 5-a \Leftrightarrow a=-1

    Jadi, diperoleh translasinya adalah \begin{pmatrix} -1\\2 \end{pmatrix}. Selanjutnya perhatikan,

    \begin{array}{rl} \begin{pmatrix} x'\\y' \end{pmatrix} &= \begin{pmatrix} 2\\1 \end{pmatrix} + \begin{pmatrix} -1\\2 \end{pmatrix} = \begin{pmatrix} 1\\3 \end{pmatrix}\\ \begin{pmatrix} x''\\y'' \end{pmatrix} &= \begin{pmatrix} 2h-x'\\y' \end{pmatrix} + \begin{pmatrix} 2(3)-1\\3 \end{pmatrix} = \begin{pmatrix} 5\\3 \end{pmatrix}. \end{array}

    JAWABAN : A

  5. \displaystyle{\int} \dfrac{3(1-x)}{1+\sqrt{x}} ~dx= \ldots

    A. 3x-2x\sqrt{x}+C

    B. 2x-3x\sqrt{x}+C

    C. 3x\sqrt{x}-2x+C

    D. 2x\sqrt{x}-3x+C

    E. 3x+2x\sqrt{x}+C

    PEMBAHASAN.

    NOTE : a-b = (\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})

    Perhatikan,

    \begin{array}{rl} \displaystyle{\int} \dfrac{3(1-x)}{1+\sqrt{x}} ~dx &= \displaystyle{\int} \dfrac{3(1-\sqrt{x})(1+\sqrt{x})}{1+\sqrt{x}} ~dx\\ &= \displaystyle{\int} 3(1-\sqrt{x}) ~dx\\ &= \displaystyle{\int} 3-3\sqrt{x} ~dx\\ &= \displaystyle{\int} 3-3x^{\frac{1}{2}} ~dx\\ &= 3x-\dfrac{3}{\frac{3}{2}} x^{\frac{3}{2}} + C\\ &= 3x-2x^{\frac{3}{2}} + C\\ &= 3x-2 \cdot x \cdot x^{\frac{1}{2}} + C\\ &= 3x-2x\sqrt{x}+C. \end{array}

    JAWABAN : A

  6. Jika kurva f(x) =ax^2+bx+c memotong sumbu-y di titik (0,1) dan \lim_{x \to 1} \dfrac{f(x)}{x-1} = -4, maka \dfrac{b+c}{a} = \ldots

    A. -1

    B. -\dfrac{1}{2}

    C. 0

    D. 1

    E. \dfrac{3}{2}

    PEMBAHASAN.

    Kurva f(x) memotong sumbu-y di titik (0,1) artinya

    \begin{array}{rl} f(0) &= a(0)^2+b(0)+c\\ 1&=c \ldots \text{ (i)} \end{array}

    Selanjutnya dengan menggunakan Dalil L’Holpital, didapat

    \begin{array}{rl} \lim_{x \to 1} \dfrac{ax^2+bx+c}{x-1} &= -4\\ \lim_{x \to 1} \dfrac{2ax+b}{1} &= -4\\ 2a(1)+b &= -4\\ 2a+b &= -4 \ldots \text{ (ii)} \end{array}

    Kemudian karena \lim_{x \to 1} \dfrac{f(x)}{x-1} = -4, artinya f(1)=0. Sehingga diperoleh

    \begin{array}{rl} f(1) &= a(1)^2+b(1)+c\\ 0&=a+b+c \ldots \text{ (iii)} \end{array}

    Substitusi persamaan (i) ke persamaan (iii), diperoleh

    a+b = -1 \ldots \text{ (iv)}

    Eliminasi persamaa (ii) dan persamaan (iv), diperoleh

    \begin{array}{l} 2a+b=-4\\ \underline{a+b=-1}~~-\\ a=-3.\end{array}

    \dfrac{b+c}{a} = \dfrac{2+1}{-3} = -1.

    JAWABAN : A

  7. Banyak susunan berfoto berjajar untuk 3 pasang pemain bulutangkis ganda dengan tidak setiap pemain dan pasangannya berdekatan adalah …

    A. 720

    B. 705

    C. 672

    D. 48

    E. 15

    PEMBAHASAN.

    Banyak susunan foto pemain bulutangkis dengan posisi sebarang, yaitu 6!=1 \times 2 \times 3 \times 4 \times 5 \times 6 = 720. Selanjutnya banyak kemungkinan foto bersama dengan setiap pasangan berdekatan (asumsikan 1 pasangan adalah 1 objek, berarti ada 3 objek), yaitu 3!=1 \times 2 \times 3 = 6. Karena setiap pasangan bisa menukar posisi, maka didapat 2 \times 2 \times 2 = 8. Sehingga banyak susunan foto untuk setiap pasangan dengan posisi berdekatan adalah 6 \times 8 = 48. Karena tidak setiap pemain dan pasangannya berdekatan, maka banyak kemungkinannya adalah 720-48 = 672 cara.

    JAWABAN : C

Untuk file PDF, silahkan download DISINI dan Tes Potensi Akademik lengkapnya ada DISINI.
NOTE : silahkan dikoreksi dan berikan komentar jika ada kesalahan atau masih ada keambiguan baik dalam soal maupun penyelesaian soal ini.

5 comments on “Pembahasan TKPA Matematika Dasar SBMPTN 2017 (Kode Soal 226) (2)”

  1. Hallow, gan.

    Mohon maaf, untuk nomor 1 di atas, jawabannya D ya?

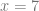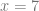    Coba substitusi x = 7, memang hasil komposisinya 3, akan tetapi daerah asal fungsi komposisinya adalah x \leq 5 , sehingga x = 7 tidak bisa kita substitusikan ke fungsi komposisinya. Mohon pencerahannya!!!!

    Coba lihat alternatif penjelasan di link berikut ini :

    Pembahasan daerah hasil

    Salam blogger dan salam matematika.

    Balas

  2. Hallo selamat siang bapak aim perkenalkan nama saya Iven Ganesja saya dari Quipper Indonesia, kami ingin mengajak bapak untuk bekerja sama dalam program Quipper Edupreneur , apa bapak ada waktu untuk mengobrol dan kalau tidak keberatan apa bapak bersedia memberikan kontak bapak misalkan email ? thank you

    Balas

Tinggalkan komentar