Sifat :
Jika (x) = xn, dengan n bilangan-bilangan bulat positif maka
(x)= nxn-1 yakni Dx(xn)= nxn-1.
Bukti :
(x)= xn
ln-kan kedua ruas, sehingga diperoleh
ln (x) = ln xn
ln (x) = n ln x
Dx(ln (x)) = Dx(n ln x)
INGAT : Dx(ln x) =
d(f(x)) = n
dx
= n
= n
= n.xn-1

Ping-balik: Turunan Fungsi dan Sifat-Sifatnya | Math IS Beautiful
sangat jelas sekali..nice post 🙂 thx
kalau turunan dari x pangkat x apa ya???
Ping-balik: turunan x^x | Math IS Beautiful
ga ada contoh nya nih ?
kalo turunan dari f(x) = ( x^3 + 5x^2 + 2x + 7 )^6
^ = pangkat
ini bisa pakai turunan aturan rantai
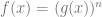 maka
maka 

Jadi,
min, tolong dibantu jawab ini dong, tan^3(sint^2). gmn cara nya thu min ? thx 🙂
Maaf sya belum tau kalo fungsinya seperti itu
Turunan:
A. y=log(sin2x/x)
B. y=10^x^2
C.y= x•e^-x cos (Πx)
ini bisa jadi rujukan materi ttg soal ini :
Ping-balik: Kuy Belajar Matematika !!!
Ping-balik: Pos blog pertama – Kuy Belajar Matematika !!!