Jan 19 2015

Matriks Invers Tergeneralisasi


Untuk mencari invers tergeneralisasi dari suatu matriks, disini akan menggunakan bantuan sebuah teorema, yaitu :

Teorema 1.

Misalkan A adalah matriks berukuran m \times n dan PAQ = \begin{bmatrix} B&0\\ 0&0 \end{bmatrix}, B adalah matriks nonsingular berukuran r \times r. Jika X adalah matriks berukuran n \times m yang didefinisikan sebagai X = Q\begin{bmatrix} Z&U\\ V&W \end{bmatrix}P dengan U,V,W dan Z adalah matriks sebarang, maka X adalah matriks invers tergeneralisasi jika dan hanya jika Z=B^{-1}.

Contoh 2.

Diketahui matriks A = \begin{bmatrix} 1 & 0 & 1 & 1\\ 0 & 1 & -1 & 0\\ 1 & 1 & 0 & 1\\\end{bmatrix}. Carilah matriks invers tergeneralisasi atau A^g.

  1. Pertama dibuat matriks augmentasinya dengan matriks I_3. Setelah itu, akan dilakukan OBE untuk mencari matriks P. Dalam hal ini, matriks P adalah matriks hasil OBE sampai menghasilkan eselon baris.

    \begin{bmatrix} 1 & 0 & 1 & 1 &| & 1 & 0 & 0\\ 0 & 1 & -1 & 0 &| & 0 & 1 & 0\\ 1 & 1 & 0 & 1 &| & 0 & 0 & 1\\ \end{bmatrix} \begin{array}{c} \\ \\ B_3-B_1\\ \end{array}

    \begin{bmatrix} 1 & 0 & 1 & 1 &| & 1 & 0 & 0\\ 0 & 1 & -1 & 0 &| & 0 & 1 & 0\\ 0 & 1 & -1 & 0 &| & -1 & 0 & 1\\ \end{bmatrix} \begin{array}{c} \\ \\ B_3-B_2\\ \end{array}

    Diperoleh matriks P = \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ -1 & -1 & 1\\ \end{bmatrix}

    Setelah itu, matriks hasil OBE di atas ditranpose dan dibuat matriks augmentasi dengan matirks I_4. Kemudian dilakukan OBE lagi sampai menghasilakn matriks eselon baris tereduksi, matriks inilah yang merupakan matriks Q.

    \begin{bmatrix} 1 & 0 & 1 & 1 &| & 1 & 0 & 0\\ 0 & 1 & -1 & 0 &| & 0 & 1 & 0\\ 0 & 0 & 0 & 0 &| & -1 & -1 & 1\\ \end{bmatrix} \begin{array}{c} \\ \mbox{transpose}\\ \\ \end{array}

    \begin{bmatrix} 1 & 0 & 0 & | & 1 & 0 & 0 & 0\\ 0 & 1 & 0 & | & 0 & 1 & 0 & 0\\ 1 & -1 & 0 &| & 0 & 0 & 1 & 0\\ 1 & 0 & 0 & | & 0 & 0 & 0 & 1\\ \end{bmatrix} \begin{array}{c} \\ \\ B_3-B_1\\ B_4-B_1\\ \end{array}

    \begin{bmatrix} 1 & 0 & 0 & | & 1 & 0 & 0 & 0\\ 0 & 1 & 0 & | & 0 & 1 & 0 & 0\\ 0 & -1 & 0 &| & -1 & 0 & 1 & 0\\ 0 & 0 & 0 & | & -1 & 0 & 0 & 1\\ \end{bmatrix} \begin{array}{c} \\ \\ B_3+B_2\\ \\ \end{array}

    \begin{bmatrix} 1 & 0 & 0 & | & 1 & 0 & 0 & 0\\ 0 & 1 & 0 & | & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & | & -1 & 1 & 1 & 0\\ 0 & 0 & 0 & | & -1 & 0 & 0 & 1\\ \end{bmatrix}

    Diperoleh matriks Q = \begin{bmatrix} 1 & 0 & -1 & -1\\ 0 & 1 & 1 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}. Jadi, matriks P = \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ -1 & -1 & 1\\ \end{bmatrix} dan Q = \begin{bmatrix} 1 & 0 & -1 & -1\\ 0 & 1 & 1 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}.

  2. Cek apakah PAQ = \begin{bmatrix} I_r & O\\ O & O\end{bmatrix} (hanya untuk mengecek bahwa matriks P dan Q yang diperoleh tersebut sudah benar).

  3. Misal X' = \begin{bmatrix} I_r & U\\ V & W\end{bmatrix}.

    Pilih matriks U, V \mbox{ dan } W sebagai berikut :

    U = \begin{bmatrix} 1\\ 1\end{bmatrix}

    V = \begin{bmatrix} 1&2\\ 1&1\end{bmatrix}

    W = \begin{bmatrix} 1\\ 2\end{bmatrix}

    Sehingga diperoleh

    X' = \begin{bmatrix} 1 & 0 & 1\\ 0 & 1 & 1\\ 1 & 2 & 1\\ 1 & 1 & 2\end{bmatrix}

    Berakibat

    X = QX'P

    = \begin{bmatrix} 1 & 0 & -1 & -1\\ 0 & 1 & 1 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 1\\ 0 & 1 & 1\\ 1 & 2 & 1\\ 1 & 1 & 2\end{bmatrix} \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ -1 & -1 & 1\\ \end{bmatrix}

    = \begin{bmatrix} 1 & 0 & -1 & -1\\ 0 & 1 & 1 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 0 & -1 & 1\\ -1 & 0 & 1\\ 0 & 1 & 1\\ -1 & -1 & 2\end{bmatrix}

    = \begin{bmatrix} 1 & -1 & 2\\ -1 & 1 & 2\\ 0 & 1 & 1\\ -1 & -1 & 2\end{bmatrix}

  4. Cek apakah AXA = A

    AXA = \begin{bmatrix} 1 & 0 & 1 & 1\\ 0 & 1 & -1 & 0\\ 1 & 1 & 0 & 1\\\end{bmatrix} \begin{bmatrix} 1 & -1 & 2\\ -1 & 1 & 2\\ 0 & 1 & 1\\ -1 & -1 & 2\end{bmatrix} \begin{bmatrix} 1 & 0 & 1 & 1\\ 0 & 1 & -1 & 0\\ 1 & 1 & 0 & 1\\\end{bmatrix}

    = \begin{bmatrix} 1 & 0 & 1 & 1\\ 0 & 1 & -1 & 0\\ 1 & 1 & 0 & 1\\\end{bmatrix} \begin{bmatrix} -1 & -3 & 2 & -1\\ 1 & 3 & -2 & 1\\ 1 & 2 & -1 & 1\\ 1 & 1 & 0 & 1\end{bmatrix}

    = \begin{bmatrix} 1 & 0 & 1 & 1\\ 0 & 1 & -1 & 0\\ 1 & 1 & 0 & 1\\\end{bmatrix}

    = A

  5. Jadi, X = \begin{bmatrix} 1 & -1 & 2\\ -1 & 1 & 2\\ 0 & 1 & 1\\ -1 & -1 & 2\end{bmatrix} merupakan invers tergeneralisasi dari matriks A tersebut.

 

13 comments on “Matriks Invers Tergeneralisasi”

  6. Halo mas, saya riama.
    Mas saya mau nanya, contoh di atas kan ukuran matriks A= 3 x 4, untuk mencari matriks P digunakan formula B3-B1 dan B3-B2.. dan untuk mencari Q digunakan B4-B1; B3-B1 dan B3+B2 itu ketentuannya seperti apa ya mas? soalnya saya mau mengolah matriks yang berukuran lebih besar..
    Terimakasih mas 🙂

    Balas

  8. Mau tanya min, untuk paq = b 0 0 0 nah ketika d cntoh soal knp jd Identitas? Dan yg x’ = u v w z, d postingan sblm nya z adalah invers dr b tp d cntoh soal z menjadi Identitas. Bisa tlg d jlskan? Saya kurang paham. Terimakasih untuk postingannya 🙂

    Balas

    • B adalah matriks non-singular, yaitu matriks yg determinannya tidak sama dengan nol. Jika saya ambil B nya matriks identitas, apakah melanggar pernyataannya ? Tidak kan ?
      Nah, sya menggunkaan matriks identitas agar utk mempermudah aja. Krena nanti qta akan mencari matriks Z, dmn Z adalah invers dari B.

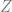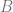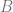      Kmudian utk pertanyaan kedua, karena Z adalah invers B dan B nya matriks identitas, maka dpat 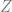Z nya itu matriks identitas juga.

      Balas

Tinggalkan komentar