-
Akar-akar persamaan kuadrat 5x2 – 3x + 1 = 0 adalah …
A. imajiner
B. kompleks
C. nyata, rasional dan sama
D. nyata dan rasional
E. nyata, rasional dan berlainan.
PEMBAHASAN :
NOTE : D > 0, memiliki akar-akar riil dan berbeda
D < 0, memiliki akar-akar imajiner
D = 0, memiliki akar-akar riil dan kembar
D = b2 – 4ac
= (-3)2 – 4.5.1
= 9 – 20
= -11
JAWABAN : A
-
Hasil kali akar-akar persamaan kuadrat 6x2 – 2x + 3 = 0 adalah …
A. 3
B. 2
C. 1/2
D. –1/2
E. -2
PEMBAHASAN :
6x2 – 2x + 3 = 0
x1.x2 =
=
=
JAWABAN : C
-
Akar-akar persamaan kuadrat x2 + 3x – 2 = 0 adalah x1 dan x2. Nilai
+
= …
A. –2/3
B. –3/2
C. 2/3
D. 3/2
E. 5/2
PEMBAHASAN :
+
=
=
=
= –
= –
=
JAWABAN : D
-
Akar-akar persamaan kuadrat x2 – x + 3 = 0 adalah x1 dan x2. Persamaan kuadrat dengan akar-akar (x1 + 2) dan (x2 + 2)adalah …
A. x2 – x + 9 = 0
B. x2 + 5x + 9 = 0
C. x2 – 5x – 9 = 0
D. x2 – 5x + 5 = 0
E. x2 – 5x + 9 = 0
PEMBAHASAN :
PK Baru : x2 – (y1 + y2)x + y1.y2 = 0
y1 + y2 = (x1 + 2) + (x2 + 2)
= (x1 + x2) + 4
= –
+ 4
= –
+ 4
= 5
y1 . y2 = (x1 + 2)(x2 + 2)
= x1.x2 + 2x1 + 2x2 + 4
= x1.x2 + 2(x1 + x2) + 4
=
– 2
+ 4
=
– 2
+ 4
= 3 + 2 + 4
= 9
PK Baru : x2 – 3x + 8 = 0
JAWABAN : E
-
Sumbu simetri parabola y = x2 – 5x + 3 diperoleh pada garis …
A. x = 3/2
B. x = 3/2
C. x = 5/2
D. x = 5/2
E. x = 3
PEMBAHASAN :
Karena sumbu simetri parabola pasti dilewati oleh titik puncak parabola, maka kita bisa peroleh dengan y’ = 0
Y’ = 2x – 5
0 = 2x – 5
x = 5/2
jadi sumbu simetri parabola y = x2 – 5x + 3 adalah x = 5/2
JAWABAN : D
-
Ordinat titik balik maksimum grafik fungsi y = -x2 – (p – 2)x + (p – 4) adalah 6. Absis titik balik maksimum adalah …
A. –4
B. –2
C. – 1/6
D. 1
E. 5
PEMBAHASAN :
NOTE : ordinat = sumbu-y, absis = sumbu-x
Karena berbicara titik balik maksimum, maka kita manfaatkan turunan pertama yaitu y’ = 0
-2x – (p – 2) = 0
-2x = p – 2
x =
sehingga diperoleh titik balik maksimum = (
, 6), substitusi titik balik maksimum ke fungsi y.
6 = -(
)2 – (p – 2)
+ (p – 4)
6 = -(
) –
+
+ (p – 4) [kalikan 4 kedua ruas]
24 = -(4 – 4p + p2) – (4p – 2p2) + (8 – 4p) + (4p – 16)
24 = -4 + 4p – p2 – 4p + 2p2 + 8 – 4p + 4p – 16
0 = p2 – 36
p2 = 36
p1 = 6 atau p2 = -6
unutk p = 6
x =
= -2
unutk p = -6
x =
= 4
JAWABAN : B
-
Nilai minimum fungsi f(x) = x2 – 5x + 4 adalah ….
A. –9/4
B. 9/4
C. 5/2
D. -5/2
E. 4
PEMBAHASAN :
Perlu dicatat bahwa nilai maksimum atau minimum suatu fungsi pasti berhubungan dengan turunan pertama yaitu f'(x) = 0
2x – 5 = 0
x =
f(
) = (
)2 – 5.
+ 4
=
–
+ 4
=
–
+
= –
JAWABAN : A
-
Fungsi kuadrat yang grafiknya berpuncak dititik (2, 3) dan melalui titik (-2, 1) adalah …
A. y = -1/8(x – 2)2 + 3
B. y = -1/8(x – 2)2 – 3
C. y = 1/8(x + 2)2 – 3
D. y = 1/8(x + 2)2 + 3
E. y = 1/8(x – 2)2 + 3
PEMBAHASAN :
f(x) = ax2 + bx + c
f'(x) = 2ax + b
0 = 2a.2 + b
0 = 4a + b
-b = 4a … (i)
nilai fungsi pada titik puncak
f(2) = a(2)2 + b.2 + c
3 = 4a + 2b + c
3 = -b + 2b + c
3 = b + c … (ii)
f(-2) = a(-2)2 + b(-2) + c
1 = 4a – 2b + c
1 = -b – 2b + c
1 = -3b + c … (iii)
eliminasi persamaan (ii) dan (iii)
b + c = 3
-3b + c = 1 –
4b = 2
b = 1/2
substitusi b = 1/2 ke persamaan (ii)
1/2 + c = 3
c = 5/2
substitusi b = 1/2 ke persamaan (i)
-1/2 = 4a
a = -1/8
f(x) = (-1/8)x2 + 1/2 x + 5/2
= (-1/8)x2 + 4/8 x + 5/2
= -1/8(x2 – 4x) + 5/2
= -1/8(x – 2)2 + 4/8 + 5/2
= -1/8(x – 2)2 + 4/8 + 20/8
= -1/8(x – 2)2 + 3
JAWABAN : A
-
Akar-akar persamaan kuadrat 2x2 – 13x + 15 = 0 adalah …
A. 3/2 dan 6
B. 3/2 dan 5
C. 1 dan 6
D. 2 dan 3
E. 2 dan 3/2
PEMBAHASAN :
gunakan Rumus Kecap
x1,2 =
=
=
=
=
x1 =
= 5
x2 =
=
JAWABAN : B
-
Akar-akar persamaan kuadrat x2 – 3x – 2 = 0 adalah x1 dan x2. Persamaan kuadrat dengan akar-akar (x1 + 2) dan (x2 + 2) adalah …
A. x2 + 2x + 7 = 0
B. x2 – 2x – 7 = 0
C. x2 – 2x – 5 = 0
D. x2 – 7x + 8 = 0
E. x2 + 7x + 8 = 0
PEMBAHASAN :
PK Baru : x2 – (y1 + y2)x + y1.y2 = 0
y1 + y2 = (x1 + 2) + (x2 + 2)
= (x1 + x2) + 4
= –
+ 4
= –
+ 4
= 7
y1 . y2 = (x1 + 2)(x2 + 2)
= x1.x2 + 2x1 + 2x2 + 4
= x1.x2 + 2(x1 + x2) + 4
=
– 2
+ 4
=
– 2
+ 4
= -2 + 6 + 4
= 8
PK Baru : x2 – 7x + 8 = 0
JAWABAN : D
-
Diketahui x1 dan x2 adalah akar-akar persamaan kuadrat x2 + 4x + (a – 4) = 0. Jika x1 = 3x2, maka nilai a yang memenuhi adalah …
A. 1
B. 3
C. 4
D. 7
E. 8
PEMBAHASAN :
x1 + x2 = -4
3x2 + x2 = -4
4x2 = -4
x2 = -1
x1 + (-1) = -4
x1 = -3
PK : x2 – (x1 + x2)x + x1.x2 = 0
x2 – (-3 – 1)x + (-3)(-1) = 0
x2 + 4x + 3 = 0
a – 4 = 3
a = 7
JAWABAN : D
NOTE : silahkan dikoreksi dan berikan komentar jika ada kesalahan atau masih ada keambiguan dalam penyelesaian soal-soal ini.

Mas, saya mau tanya soal fungsi kuadrat berikut :
1. Sebuah grafik fungsi kuadrat memotong sumbu y di titik (0,1) dan (0,4) serta melalui titik (4,0)
a) tentukan rumus fungsi kuadrat tersebut dalam variable y
b) tentukan sumbu simetrinya
c) tentukan koordinat titik puncaknya
kalau biasanya kan grafik fungsi kuadrat kan terbuka ke atas atau ke bawah, tapi untuk soal berikut ini bagaimana cara menyelesaikannya kalau grafiknya terbuka ke kanan atau ke kiri ?
untuk fungsi kuadat yg kurvanya terbuka ke kiri atau kekanan, bisa qta gunakan fungsi terhadap variable y
misal :
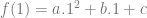 ==> 0 = a + b + c … (i)
==> 0 = a + b + c … (i)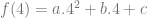 ==> 0 = 16a + 4b + c … (ii)
==> 0 = 16a + 4b + c … (ii) ==> c = 4
==> c = 4
(0, 1) ==>
(0, 4) ==>
(4, 0) ==>
substitusi c = 4 ke pers (i) dan (ii) :
a + b = -4 … (iii)
16a + 4b = -4 ==> 4a + b = -1 … (iv)
eliminasi (iii) dan (iv) shingga diperoleh
a = 1 dan b = -5
jadi
untuk bgian b dan c, gunakan = 0
= 0
mas mau tanya soal ini tolong dibales cpt yow
fungsi kuadrat pembuat 0 dari fungsi kuadrat fe=16-x kuadrat
MEI 10, 2013 @ 11:36 PM
mas mau tanya soal ini tolong dibales cpt yow
fungsi kuadrat pembuat 0 dari fungsi kuadrat fe=16-x kuadrat
no 087733767862
f(X) = 16 – x
0 = 16 – x
0 = (4 – x)(4 + x)
x=4 atau x=-4
mas klo cara untuk mencari titik potong dari persamaan y=-2×2-8x dan y=5×2+10x tlng kasih jwbnnya mas,,,,makasih yaaa
utk mencari titik ptongnya, kita samakan kedua persamaannya
.
.
.
silahkan lnjutkan sndiri y 🙂
Mas puya soal-soal menggambar grafik fungsi kudrat untuk mengukur kemampuan komunikasi matematis?
maaf, gk punya 🙂
mas, kalo ada soal gini :
garis 6x-y-5=0 memotong kurva y=x^2-kx+11 di titik puncak P(a,b). maka harga (a+b)=..
mas,kalo tahu bisa tolong di jelaskan. bila terlalu panjang, rumus2-nya saja yang dipakai utk menjawab pertanyaan tsb juga gapapa.
terimakasih
mas mau nanya ini:
pada persamaan x^2-6x+y^2-8x+11 = 0. Tentukan nilai titik P (3,b) yang berhubungan dengan lingkaran tersebut. makasih ya
mas klo soalnya sprti ini :
Permintaan : (x+10)(P+200)=300
penawaran : P = 2 + x/2
gimana ea cara cri harga keseimbangannya…??
makasih ya
terimakasih ya contoh soalnya bermanfaat banget buat latihan uts mtk, doakan berhasil ya
Maaf ini un th brp ya?
soal ini tidak berasal dari tahun yang sama